|
Cherchons un exemple de situation sur le calcul du barycentre en
gestion de stock, manutention
La méthode du barycentre.
En ligne le 12/12/2004
Localisation des
entrepôts: La notion du Barycentre. Rajouté
03/06/2005
.....Ó Objectif
La méthode du barycentre
permet de déterminer le milieu d’un réseau de points à desservir
dont les coordonnées sont pondérées par un indicateur de trafic
pouvant être exprimé en poids, volume, distance, nombre de lignes de
commandes, chiffre d’affaires...
La suite, ici
Document sur le barycentre;
téléchargeable cet exercice de transposition en logistique
Téléchargement de la partie mathématique abordée ci-dessous
Nouvel exercice, ici
|
La notion de
Barycentre abordée de manière concrète en S ( 1 ) |
Par Vincent Lesage, professeur au
Lycée M. Van der Meersch de Roubaix, juin 2001.
Nous devons beaucoup à Archimède de
Syracuse (287 - 212 Av. J.C.), qui a défriché et défini le
premier la notion de Barycentre, dans un cadre très concret et
intuitif.
La présentation esquissée ici s'efforce de rester fidèle à cette
conception :
Voici une haltère constituée d’une tige non pesante et de 2 masses
égales :
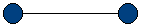
Où doit-on placer la main pour soulever l’haltère sans se tordre le
poignet ?
Evidemment au milieu !
Que devient la réponse si l’haltère se présente sous forme
dissymétrique :
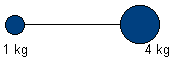
Le simple bon sens recommande de prendre l’haltère en un point de la
tige beaucoup plus proche de la masse la plus lourde :
ici 4 fois plus proche des 4 kg que de la masse de 1 kg.
Remarque : prendre d’autres unités que des kg (des livres,
des onces, etc …) n’y changerait rien !
Concrètement, il suffit de partager l’espace entre les deux boules
en 5 parties égales et de placer la main à la 4ème
graduation après 1 kg : ceci se traduit par la construction de
Thalès de type "Noeud Papillon" suivante :
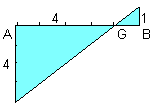
On sent que ce point G est le point d’application de la force de
pesanteur sur l’objet solide de 5 kg constitué de la tige non
pesante, de la masse de 1 kg en A et de la masse de 4 kg en B.
Du point de vue de la Mécanique des Solides (branche de la
Physique), un tel point est appelé Centre de Gravité ou Barycentre :
Baros = Poids en Grec ; Gravis = Lourd en Latin) du solide constitué
de la masse en A de 1 kg et de la masse en B de 4 kg. On
notera symboliquement ceci : (G, 5) = (A,1) (B,4)
La Construction de Thalès est équivalente à l’égalité
vectorielle correspondante :
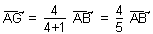
Remarquer aussi la Relation des Moments :
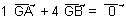
La Relation des Moments définit en Mécanique des Solides la non
rotation de l’ensemble autour de G : le Moment total est nul ó
on ne se tord pas le poignet en G.
(étymologiquement : ce qui donne le Mouvement = Movimento =
Momento de Galilée au XVIéme siècle)
Principe du Bras de Levier d' Archimède :
Le problème des haltères peut être transposé ainsi :
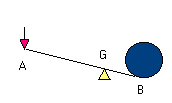
Pour soulever une charge (les 4 kg en B) avec un levier, la
force nécessaire est inversement
proportionnelle à la distance à la butée (située en G) du levier.
(Plus le bras de levier est long, moins on se fatigue ! La phrase
"Donnez moi un bras de levier, et je vous soulèverai le monde" a été
attribuée à Archimède.)
Soit : le produit de la force par le rayon est constant : on appelle
ce produit le Couple ou Moment généré par la force appliquée
au levier.
Si on veut exercer en A une force équivalente à une masse de 1 kg
pour soulever B :
le couple moteur (1 kg x GA ) équilibre exactement le couple
résistant (4 kg x GB) créé par la charge de l'autre côté.
L'équilibre des Moments fournit donc une équation (1 GA = 4 GB)
Ce qui équivaut ici à :
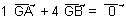
La forme vectorielle est préférable : elle est plus facilement
généralisable à d'autres configurations (attention au signe ou à
l'orientation sinon : voir la suite de l'exposé). Lien ci-dessous:
La suite:
http://www4.ac-lille.fr/~math/classes/geom/bary1s/barycentre.htm
On nous signale que le lien est inopérant.
Sinon pour aller plus loin pour mateux,
Voir:
http://fr.wikipedia.org/wiki/Barycentre
|
Nous sommes le
Vendredi 24 Mars 2017 et il est 07:16:04
PageWeb PDF Converter
pour Word.239 Ko
26.00Ko (26624 octets)
1,35 Mo
9 Ko
Graphisme
Concept: Webmestre